Banner Title Products
Solution for Unknown Loads Using Optimization Technique
In the design of long span structures, we often face a problem where we would seek a solution to unknown loading conditions necessary to satisfy a given design requirement such as shown in Figure 1.
MIDAS/Gen is capable of solving this type of problems using an optimization technique by calculating the optimum variables for given constraints and object functions. For constraint conditions, Equality and Inequality conditions are permitted. The types of object functions include the sum of the absolute values, the sum of the squares, and the maximum of the absolute values.
The sum of the absolute values
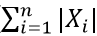The sum of the squares
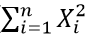The maximum of the absolute values
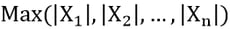
Figure 1(a) illustrates the problem of finding jack-up loads in long-span beam. An artificial moment distribution of the beam or initial displacements in the beam may be imposed as a condition.
Figure 1(b) illustrates a problem of finding leveling loads during construction in a long-span structure in which a specific deformed shape is imposed as a condition.
Figure 1(c) illustrates a cable-stayed bridge having unknown cable tensions under a dead or live load condition. The lateral displacement of the pylon is limited not to exceed a specific value, and the vertical displacements at Points B and C must be positive (+).
The above problems create equality and inequality conditions, and MIDAS/Gen solves the problems by the optimization technique.
The following describes the analysis procedure for finding the jack-up loads at Points A and B using Equality conditions, as shown in Figure 1 (a):
-
Apply a virtual (unit) load at the points of and in the direction of the unknown jack-up loads as shown in Figure 1 (a), one at a time. The number of unit load conditions created is equal to the number of unknown loads.
-
Carry out a static analysis for the design loading condition, which is a uniformly distributed load in this case.
-
Formulate Equality conditions using the constraints imposed.
-
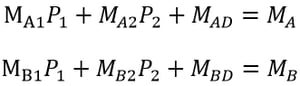
Using linear algebraic equations, the equality conditions are solved. If the numbers of the unknown loads and equations are equal, the solution can be readily obtained from the matrix or the linear algebra method.
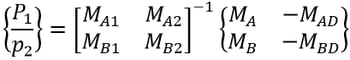
The following illustrates an analysis procedure for finding the cable tensions using inequality conditions of the structure shown in Figure 1 (c):
- Apply a virtual (unit) load in the form of a pre-tension load in each cable. The number of unit load conditions created is equal to the number of the unknown tension loads in the cables.
- Carry out a static analysis for the design loading condition, which is a uniformly distributed load in this case.
- Formulate Inequality conditions using the constraints imposed.
-
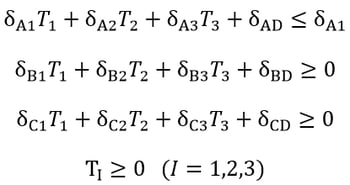
Using the optimization technique, a solution satisfying the inequality conditions is obtained. Numerous solutions to the unknown loads exist depending on the constraints imposed to the Inequality conditions. MIDAS/Gen finds a solution to Inequality conditions, which uses variables that minimize the given object functions. MIDAS/Gen allows us to select the sum of the absolute values, the sum of the squares and the maximum of the absolute values of variables for the object functions. Weight factors can be assigned to specific variables to control their relative importance, and the effective ranges of the variables can be specified.
A comprehensive understanding of a structure is required to use the above optimization technique for finding necessary design variables. Since Equality or Inequality conditions may not have a solution depending on the constraints, selection of appropriate design conditions and object functions are very important.
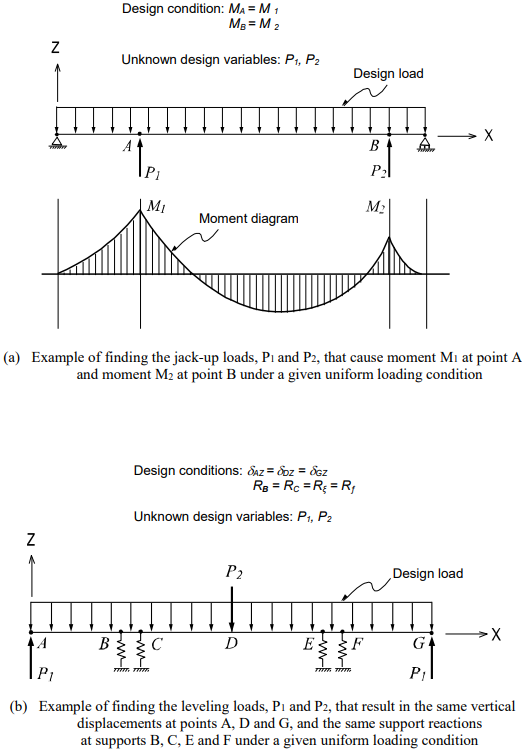
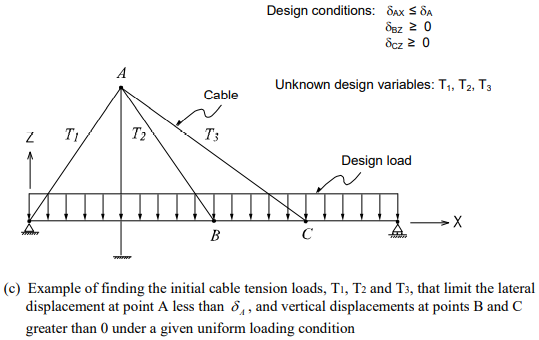
Figure 1. Examples of Finding Unknown Loads that Satisfy Various Design Conditions
