Banner Title Products
OVERVIEW
In a certain concrete structure with considerable mass or where a construction progresses rapidly with a number of construction joints, the rate and amount of heat generation due to hydration are important. Non-uniform thermal expansion and contraction due to heat of hydration and cooling of concrete accompanied by changing constraints create undesirable stresses. The stresses may cause detrimental cracking in the concrete, thereby reducing its strength and durability.
Heat of hydration analysis thus becomes important when casting mass concrete structures. It enables us to predict and control temperature and stress distribution within a structure to avoid potential problems. Mass concrete structures requiring heat of hydration analysis depend on their dimensions, shapes, cement types and construction conditions.
In practice, hydration analyses are normally carried out for slabs or mats in excess of 800~1000mm in thickness and walls confined at bottom in excess of about 500mm. Surface cracking may develop initially due to the temperature difference between the surface and center. Through-cracks can also develop as a result of contraction restrained by external boundary conditions in the cooling process of high heat of hydration.
The heat of hydration analysis is largely classified into several sub-analyses. It entails temperature distribution analysis for conduction, convection, heat source, etc.; change in modulus of elasticity due to curing and maturity; and stress analysis for creep and shrinkage. The following outlines the various components affecting the analysis.
Contents
3. Procedure for Heat of Hydration Analysis
Heat Transfer Analysis
MIDAS/Gen calculates changes in nodal temperatures with time due to conduction, convection and heat source in the process of cement hydration. The following outlines pertinent items considered in MIDAS/Gen and some of the main concepts in heat transfer analysis:
Conduction
Conduction is a type of heat transfer accompanied by energy exchange. In the case of a fluid, molecular movements or collisions and in the case of solid, movements of electrons cause the energy exchange from a high-temperature zone to a low-temperature zone. The rate of heat transfer through conduction is proportional to the area perpendicular to heat flux multiplied by the temperature gradient in that direction (Fourier’s law).
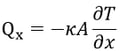
where,
In general, the thermal conductivity of saturated concrete ranges between 1.21~ 3.11, and its unit is kcal/h⋅m⋅℃. The thermal conductivity of concrete tends to decrease with increasing temperature, but the effect is rather insignificant in the ambient temperature range.
Convection
Convection is another form of heat transfer whereby heat is transmitted between a fluid and the surface of a solid through a fluid’s relative molecular motion. Heat transfer by forced convection occurs in the case where a fluid is forced to flow on a surface such that an artificial fluid current is created.
If the fluid current is naturally created by a difference in density due to a temperature difference within the fluid thereby inducing a buoyancy effect, the form of heat transfer is referred to as free convection. Because the fluid’s current affects the temperature field in this type of heat transfer, it is not a simple task to determine the temperature distribution and convection heat transfer in practice.
From an engineering perspective, the heat transfer coefficient, hc is defined to represent the heat transfer between a solid and a fluid, where T represents the surface temperature of the solid, and the fluid flowing on the surface retains an average temperature, T∞.
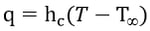
The heat transfer coefficient (hc) widely varies with the current type, geometric configuration and area in contact with the current, physical properties of the fluid, average temperature on the surface in contact with convection, location and many others, and as such it is extremely difficult to formulate the coefficient. In general, convection problems associated with temperature analyses of mass concrete structures relate to the type of heat transfer occurring between the concrete surface and atmosphere. Accordingly, the following empirical formula is often used, which is a function of an atmospheric wind speed.
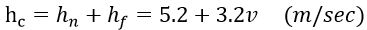
The unit for heat transfer coefficients (Convection coefficients) is kcal/m2⋅h⋅℃.
Heat Source
Heat source represents the amount of heat generated by a hydration process in mass concrete. Differentiating the equation for adiabatic temperature rise and multiplying the specific heat and density of concrete obtain the internal heat generation expressed in terms of unit time and volume. Adiabatic conditions are defined as occurring without loss or gain of heat; i.e., as isothermal.
Internal heat generation per unit time & volume (kcal/m3⋅h)
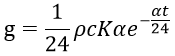
Equation for adiabatic temperature rise (℃)
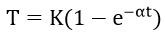where,
T∶ Adiabatic Temperature (℃)
K∶ Maximum Adiabatic Temperature Rise (℃)
α∶ Response Speed
t∶ Time (days)
Pipe Cooling
Pipe cooling is accomplished by embedding pipes into a concrete structure through which a low-temperature fluid flows. The heat exchange process between the pipes and concrete reduces the temperature rise due to the heat of hydration in the concrete, but increases the fluid temperature. The type of heat exchange is convection between the fluid and pipe surfaces. The amount of the heat exchange is expressed as follows:
Temperature
-
Ambient Temperature
Initial temperature is an average temperature of water, cement and aggregates at the time of concrete casting, which becomes an initial condition for analysis.
-
Ambient Temperature
Ambient temperature represents a curing temperature, which may be a constant, sine function or time-variant function.
-
Prescribed Temperature
A prescribed temperature represents a boundary condition for a heat transfer analysis and always maintains a constant temperature. The nodes that are not specified with convection conditions or constant temperatures are analyzed under the adiabatic condition without any heat transfer. In a symmetrical model, the plane of symmetry is typically selected as an adiabatic boundary condition. The basic equilibrium equations shown below are used for heat transfer analysis. Analysis results are expressed in terms of nodal temperatures varying with time.
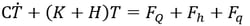
where,
T∶ Nodal Temperatue
ρ∶ Density
c∶ Specific Heat
kxx kyy kzz ∶ Heat Conductivity
h∶ Convection Coefficient
Q∶ Rate of Heat Flow-Quantity of Heat Penetrating Per Unit Time
q∶ Heat Flux-Quantity of Heat Penetrating a Unit Surface Area Per Unit Time
Thermal Stress Analysis
Stresses in a mass concrete at each stage of construction are calculated by considering heat transfer analysis results such as nodal temperature distribution, change in material properties due to changing time and temperature, time-dependent shrinkage, time and stress-dependent creep, etc. The following outlines some important concepts associated with thermal stress analysis and pertinent items considered in MIDAS/Gen.
Equivalent Concrete Age Based on Temperature and Time & Accumulated Temperature
Change in material properties occurring from the process of maturing concrete can be expressed in terms of temperature and time. In order to reflect this type of phenomenon, equivalent concrete age and accumulated temperature concepts have been incorporated. Equivalent concrete age is calculated on the basis of CEB-FIP MODEL CODE, and the Ohzagi equation is adopted for calculating accumulated temperature, which bases on a maturity theory.
- Equivalent Concrete Age as per CEB-FIP MODEL CODE
- Ohzagi’s Equation for Accumulated Temperature
Concrete Compressive Strength Calculation Using Equivalent Concrete Age and Accumulated Temperature
- ACI CODE
- CEB-FIP MODEL CODE
- Ohzagi’s Equation
- KS Concrete Code (1996)
Deformations
-
Deformations resulting from temperature changes
Thermal deformations and stresses are calculated by using the nodal temperature changes at each stage obtained through a heat transfer analysis.
-
Deformations due to shrinkage
Additional deformations and stresses develop due to shrinkage after initial curing. MIDAS/Gen adopts ACI CODE and CEB-FIP MODEL CODE to include the shrinkage effects in thermal stress analyses, which reflect the cement type, structural configuration and time.
-
Deformations due to creep
Additional deformations and stresses develop as a result of sustained stresses in concrete structures. MIDAS/Gen adopts ACI CODE and CEB-FIP MODEL CODE to consider the effects of creep.
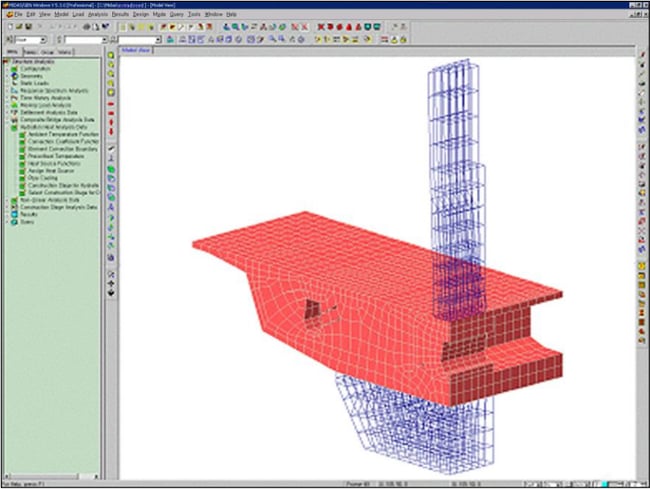
Procedure for Heat of Hydration Analysis
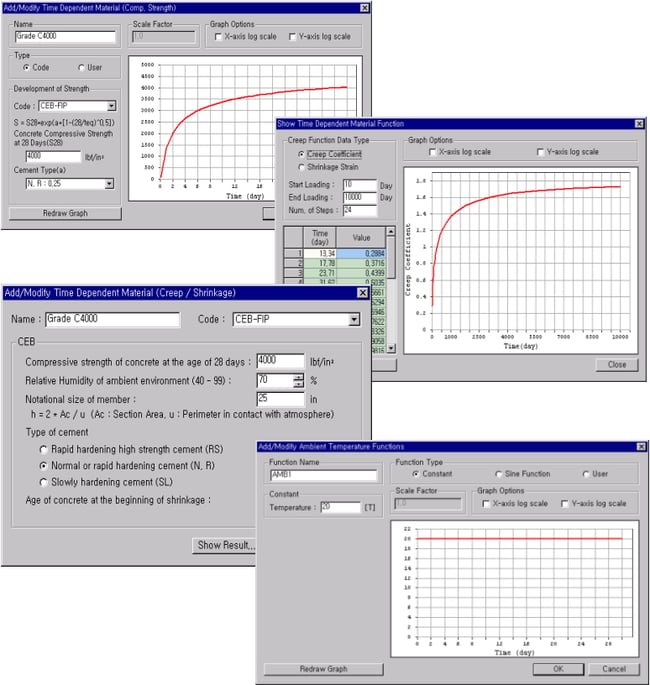
- Select Model > Properties > Time-Dependent Material (Creep/Shrinkage) and Time Dependent Material (Comp. Strength), and specify the time-dependent material properties. Link the general material properties and time-dependent material properties in Model > Properties > Time-Dependent Material Link.
- Enter the relevant data required for Heat of Hydration Analysis in the submenus of Load > Hydration Heat Analysis Data.
- Enter the Integration factor, Initial temperature, stress output points and whether or not to consider the effects of creep and shrinkage in Analysis > Hydration Heat Analysis Control.
- Select the Analysis > Perform Analysis menu or click
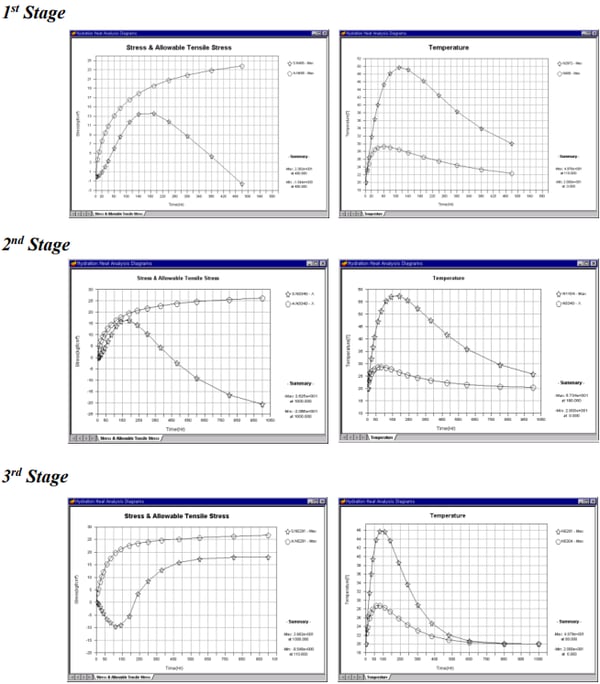
Perform analysis. - Once the analysis is completed, check the results in contours, graphs, animations, etc.
