Pre-Stressed Concrete (PSC) Analysis

MIDAS/Gen uses net cross-sections for calculating the section properties such as cross-sectional areas and bending stiffness, which account for duct areas deducted from the gross cross sections prior to jacking PS tendons. After tensioning, converted sections are used reflecting the tendon cross-sections.

The stiffness of the tendons is relatively larger than the concrete, and it results in the shift of the centroid. The eccentricities of the tendons are then calculated relative to the new centroid and their tension forces are calculated.

Rather than modeling PS tendons as truss elements or the like, MIDAS/Gen treats the tendons as equivalent pre-stressing loads, while the stiffness of the tendons is reflected in the section properties as noted above. The tensions in the tendons, which are used to calculate the equivalent loads must be based on the pre-stress losses at every construction stage caused by various factors.

MIDAS/Gen adopts the following procedure for analyzing a pre-stressed concrete structure:

1. Model the structure.
2. Activate (create) construction stages by defining time-dependent material properties and construction stages followed by defining elements, boundary conditions and loadings for each construction stage.
3. Define the tendon properties; cross-sectional area, material properties, ultimate strength, duct diameter, frictional coefficients, etc.
4. Assign the desired tendons to the section and define the tendon placement profile.
5. Define the tensions applied to the tendons and enter the tensions in the appropriate construction stages.
6. Perform the analysis

Pre-Stress Losses

• Instantaneous losses after the release

1. Anchorage slip

2. Friction between PS tendons and sheaths

3. Elastic shortening of concrete

• Long-term time-dependent losses after the release

1. Creep in concrete

2. Shrinkage in concrete

3. Relaxation of PS tendons

The frictional loss is considered in the post-tensioning but not in the pre-tensioning. The total losses for both instantaneous and long-term losses normally range in the 15~20% of the jacking force.

The most important factor for calculating the stresses of PSC (pre-stressed & post-tensioned concrete) members is the final effective pre-stress force in the tendons reflecting all the instantaneous losses and long-term losses. A relationship between and can be expressed as follows:

 

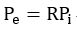
R is referred to as the effective ratio of pre-stress, which is generally for pre-tensioning and for post-tensioning.

The following outlines the pre-stress losses considered in MIDAS/Gen:

 

 

 Instantaneous Losses

1. Loss due to anchorage slip

When a PS tendon is tensioned and released, the pre-stress is transferred to the anchorage. The friction wedges in the anchorage fixtures to hold the wires will slip a little distance, thus allowing the tendon to slacken slightly. This movement, also known as anchorage take-up, causes a tension loss in the tendon in the vicinity of the anchorage. This phenomenon occurs in both post- and pre-tensioning, and overstressing the tendon can compensate it.

The loss of pre-stress due to the anchorage slip is typically limited to the vicinity of the anchorage due to the frictional resistance between the PS tendon and sheath. The effect does not extend beyond a certain distance away from the anchorage.

The tendon length l_set in the anchorage zone in Figure 1 represents the zone in which tension loss is experienced. The length is a function of the friction; if the frictional resistance is big, the length becomes shorter and vice versa. If we define the anchorage slip as Δl, tendon cross-section area as A_P, and modulus of elasticity as E_P, the following equation is established. The equation represents the shaded area in Figure 1.

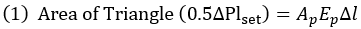
If we further define the frictional resistance per unit length as p, the pre-stress loss ΔP in Figure 1 can be expressed as

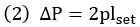
From the equations (1) and (2) above, we can derive the equation for l_set, which represents the length of the tendon being subjected to pre-stress loss due to anchorage slip.

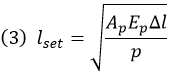
Figure 1 shows a linear distribution of tension along the length of the tendon for an illustrative purpose. MIDAS/Gen, however, considers a true nonlinear distribution of tension for calculating the pre-stress loss due to the anchorage slip.

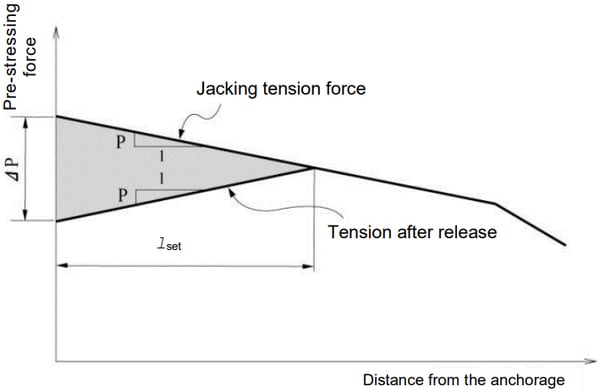
Figure 1. Effect on Pre-Stressing Force Due to Anchorage Slip

 

2. Loss due to friction between PS tendons and sheaths

In post-tensioning, frictions exist between the PS tendon and its sheathing. The pre-stressing force in the tendon decreases as it gets farther away from the jacking ends. The length effect and the curvature effect can be classified. The length effect, also known as the wobbling effect of the duct, depends on the length and stress of the tendon and refers to the friction stemming from imperfect linear alignment of the duct.

The loss of pre-stress due to the curvature effect results from the intended curvature of the tendon in addition to the unintended wobble of the duct. Frictional coefficients, μ (/radian) per unit angle and k (/m) per unit length are expressed.

If a pre-stressing force P₀ is applied at the jacking end, the tendon force P_x at a location, l away from the end with the angular change can be expressed as follows:

 

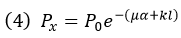
Pre-stressing Material			Wobble coefficient,	Curvature coefficient,
Bonded tendons		Wire tendons High-strength bars 7-wire strand	0.0033~0.0050 0.0003~0.0020 0.0015~0.0066	0.15~0.25 0.08~0.30 0.15~0.25
Unbonded tendons	Mastic coated	Wire tendons 7-wire strand	0.0033~0.0066 0.0033~0.0066	0.05~0.15 0.05~0.15
	Pre-greased	Wire tendons 7-wire strand	0.0010~0.0066 0.0010~0.0066	0.05~0.15 0.05~0.15

Table 1. Friction Coefficients k & µ (ACI-318)

3. Loss due to elastic shortening of concrete

As a pre-stress force is transferred to a concrete member, the concrete is compressed. The length of the concrete member is reduced, and the tendon shortens by the same amount thus reducing the tension stress. The characteristics of the elastic shortening differ slightly from pre-tensioning to post-tensioning although the two methods share the same principle.

In the case of pre-tensioning, an instantaneous elastic shortening takes place as soon as the tendon is released from the anchorage abutments, that is, when the jacking force is applied. This results in a shorter tendon and a loss of pre-tension. As shown in Figure 2, the pre-tension (Pj) in the tendon differs from the prestressing force (P_i) applied to the concrete member.

In the case of post-tensioning, pre-stressing is directly imposed against the concrete member. The process of elastic shortening is identical to the pre-tensioning method, but the tension force in the tendon is measured after the shortening has already taken place. Therefore, no tension loss occurs as a result of elastic shortening in post-tensioning. MIDAS/Gen does not consider prestress loss due to elastic shortening. As such, when a pre-stress force is specified in a concrete member where a pre-tensioning method is used, the pre-stress load (P_i) must be entered in lieu of the jacking load (Pj).

In a typical post-tensioned member, multiple tendons are placed, stressed and anchored in a pre-defined sequence. A series of concrete elastic shortenings takes place in the same member, and the pre-stress loss in each tendon changes as the pre-stressing sequence progresses. There is no tension loss in the first tendon being stressed in Figure 3 (b).

When the second tendon is tensioned as shown in Figure 3(c), a tension loss is observed in the first tendon due to the subsequent shortening from the second tensioning. Not only does MIDAS/Gen account for pre-stress loss due to elastic shortening at every construction stage, but it also reflects all pre-stress losses due to elastic shortenings caused by external forces.

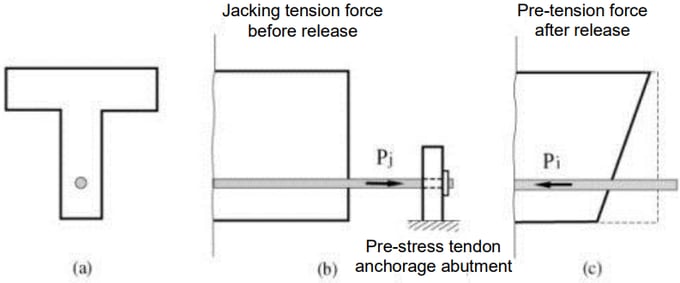Figure 2. Pre-Stress Loss Due to Elastic Shortening (Pre-Tensioned Member)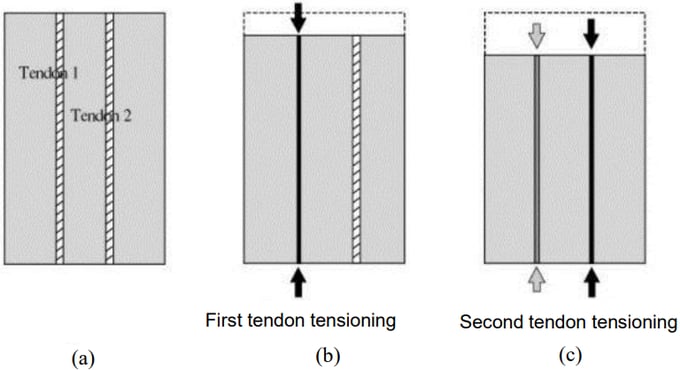

Figure 3. Pre-Stress Losses in Multi-Tendons Due to Sequential Tensioning (Post-Tensioned Member)

Pre-stress losses also occur with time due to concrete creep, shrinkage, and PS tendon relaxation. MIDAS/Gen reflects the time dependent material properties of concrete members and calculates the corresponding creep and shrinkage for all construction stages. It also accounts for pre-stress losses in PS tendons due to the changing member deformation. The pre-stress loss history can be examined for each construction stage by graphs.

Stress relaxation in steel, also termed as creep, is the loss of its stress when it is pre-stressed and maintained at a constant strain for a period of time. Pre-stress loss due to relaxation varies with the magnitude of initial stress, elapsed time in which the stress is applied, and product properties. MIDAS/Gen adopts the Magura equation for tendon relaxation.

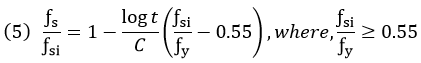
ƒ_si is initial stress; ƒ_s is the stress after loading for a period of time t ; ƒ_y is ultimate stress (0.1% offset yield stress); and C is product-specific constant. C=10 for general steel and C=45 for low relaxation steel are typically used. The above equation assumes that the stress in the tendon remains constant. In real structures, stresses in PS tendons continuously change with time due to creep, shrinkage, external loads, etc., and as such equation (5) cannot be directly applied.

Accordingly, MIDAS/Gen calculates the change in pre-stress loads in tendons due to all causes except for the relaxation itself for every construction stage and calculates the relaxation loss based on fictitious initial prestress for each construction stage.

Pre-Stress Loads

MIDAS/Gen converts the pre-stress tendon loads applied to a structure into equivalent loads as described in Figure 4 below.

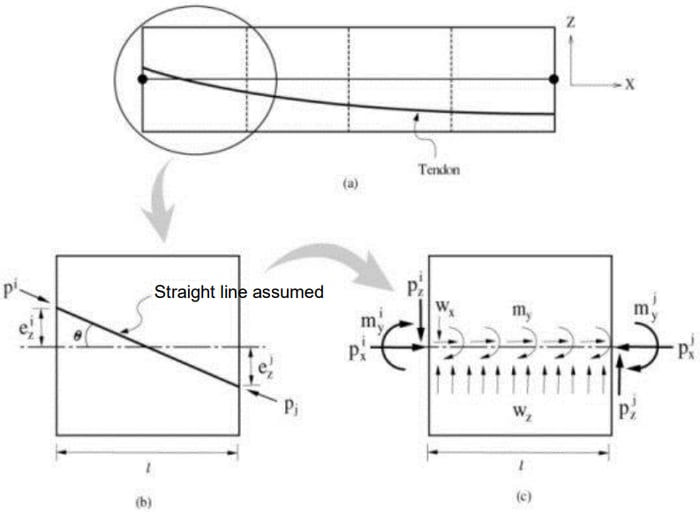Figure 4. Conversion of Pre-Stress into Equivalent Loads

Figure 4 illustrates a tendon profile in a beam element. 2-Dimension is selected for the sake of simplicity, but the process of converting into equivalent loads in the x-y plane is identical to that in the x-z plane. MIDAS/Gen divides a beam element into 4 segments and calculates equivalent loads for each segment as shown in Figure 4.

The tendon profile in each segment is assumed linear. The tension forces Pⁱ and P^j  in the tendon are unequal due to frictional loss. 3 Concentrated loads (P_x, m_ym P_z) at each end, i and j, alone cannot establish an equilibrium, and hence distributed loads are introduced for an equilibrium. Equations (1) and (2) are used to calculate the concentrated loads at each end, and Equation (3) and (4) are used to calculate the internal distributed loads.

(1)

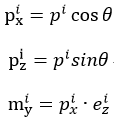
(2)

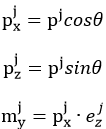(3)

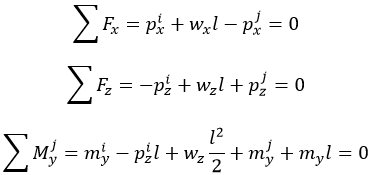(4)

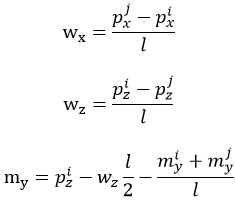
MIDAS/Gen calculates time-dependent pre-stress losses due to creep, shrinkage, relaxation, etc. for every construction stage as well as other pre-stress losses due to external loads, temperature, etc. First, the change in tension force in the tendon is calculated at each construction stage, and the incremental tension load is converted into equivalent loads, which are then applied to the element as explained above.