OVERVIEW
The ACI318M (US codes) and AS3600 (Australian codes) are very similar in basic approach. In the current documents, but, there is a number of significant differences. Through this brief document, you can discover the differences between the two codes, understand their factors and design concepts.
In this document, a comparison between ACI 318M and AS3600 Code has 5 classified sections such as 1. Strength reduction factor, 2. Concrete rectangular stress block, 3. Strength Design in shear, 4. PM interaction, 5. Development length. In addition, the specific standards are based on the ACI318M-14 standards for US Codes, and AS3600:2018 for Australian codes.
Strength Reduction Factor
The strength reduction factors are the same concept in both codes and ACI 318M-14 has different strength reduction factors for spirals (0.75) and rectangular ties (0.65), in compression controlled sections, and has 0.90 for the largest value for tension controlled section, besides 0.85 for AS3600.
And, ACI 318M applies an additional reduction factor to concrete stresses for sections under uniform compression, as an allowance for unspecified load eccentricity, whereas AS 3600 specifies a minimum eccentricity.
You can check the strength reduction factor (Ф) between each standard in the table below.
|
Building Code |
AS3600:2018 |
ACI318M-14 |
|
Axial Force Without Bending (Tension) |
0.85 (for Class N reinforcement) |
0.65 (& 0.75) to 0.90 Transition1: 0.65+0.25(εt-εty_/(0.005-εty) Transition2: 0.75+0.15(εt-εty_/(0.005-εty)
Transition1: for ties(fitments) reinforcement Transition2: for spirals(helices) reinforcement |
|
Axial Force Without Bending (Compression) |
0.65 |
|
|
Bending Without Axial Forces |
0.65 to 0.85 Transition: 1.24-13kuo/12 (for Class N reinforcement) |
|
|
Shear and Torsion |
0.75 (for Class N fitments are provided / (i) conditions) |
0.75 |
Concrete Rectangular Stress Block
You can check the strength reduction factor (Ф) between each standard in the table below.
One of the most significant is in the definition of the concrete rectangular compressive stress block, for the determination of the ultimate bending strength of beams.
The compressive stress block is an approximation to the actual stress distribution in a reinforced concrete member that takes advantage of the fact that the stress-strain curve of low to medium strength concrete has a wide plateau region where the maximum stress is maintained constant with increasing strain. In Section 8 of AS3600:3600 code, the factors were defined as;
Where α2 is the factor on the compressive stress and γ is the factor on the depth of the stress block. This variable is similar to the formula of the Canadian concrete standard (CAN-A23.3-04), and the upper limit (0.85) for the γ factor has been removed compared to the formula of the existing Australian code (AS3600-2009). In ACI 318M code, α2 and γ factor of AS3600 code are the same concepts as α2 and β1 factor respectively.
So, look at the comparison table below.
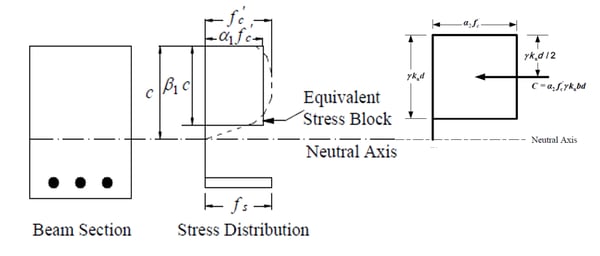
|
Building Code |
AS3600:2018 |
ACI318M-14 |
|
α2 (α1 for ACI code) |
0.85-0.0015 f’c ≥ 0.67 |
0.85 |
|
γ (β1 for ACI code) |
0.97-0.0025 f’c≥0.67 |
0.85 (fc ' ≤ 28) 0.85-0.05 (fc ' - 28) / 7 ≥ 0.65 |
|
εcu (Ultimate strain of concrete) |
0.0030 |
0.0030 |
Table 1. Comparison of Equivalent Rectangular Stress Block Factor
Note: f’c in MPa
Comparing α2 (Stress factor) and γ (Stress block depth factor) of AS3600: 2018 & ACI318M-14 between the two codes by concrete grade is as follows.
The graphs on the next page compare the stress block depth factor (Gamma) and the concrete stress factor (Alpha2) for AS 3600 and ACI 318M.
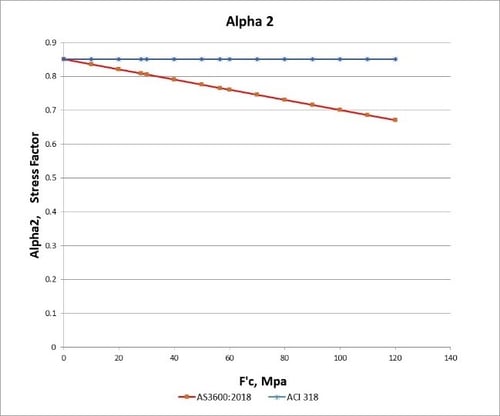 Figure 2a. Concrete Stress Factor (α2)
Figure 2a. Concrete Stress Factor (α2)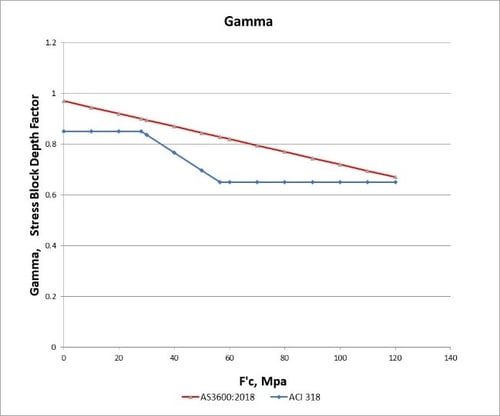 Figure 2b. Stress Block Depth Factor (γ)
Figure 2b. Stress Block Depth Factor (γ)
The concrete stress factor (alpha2) shall be assumed uniformly distributed over an equivalent compression zone bounded by edges of the cross-section
The concrete stress factor (alpha2) applicable to the rectangular stress block in AS3600:2018 is decreases linearly from 0.85 as the concrete grade increases. In ACI 318M, but, the factor remains constant for all concrete grades, 0.85.
The Stress block depth factor (gamma2) for equivalent rectangular concrete stress distribution in AS3600:2018 is decreases linearly from 0.97 as the concrete grade increases. In ACI 318M, but, this value is 0.85 for the concrete grade below 28 MPa, and 0.65 for the concrete grade above 56 MPa. The values in between concrete grades use linear interpolation.
The combined effect of variation in the two factors is shown in the graphs below. The product of Gamma and Alpha2 is proportional to the force per unit width, and is referred to below as the Force Factor. The product of the Force Factor and (1 – Gamma/2) is proportional to the moment per unit width, and is referred to the Moment Factor.
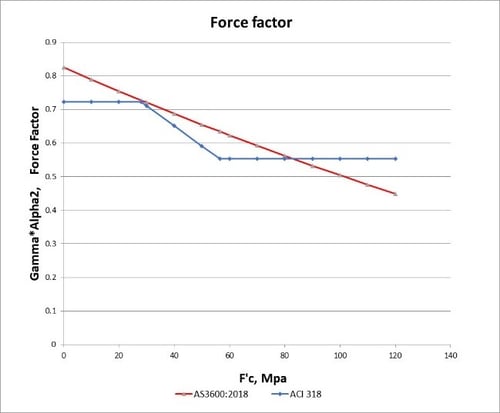 Figure 3a. Force Factor vs Concrete Grade
Figure 3a. Force Factor vs Concrete Grade
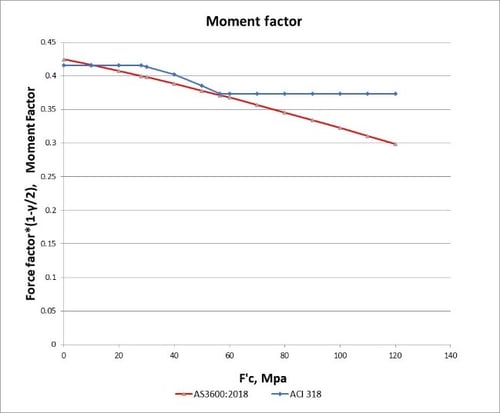 Figure 3b. Moment Factor vs Concrete Grade
Figure 3b. Moment Factor vs Concrete Grade
It can be seen that the force factor (α2*γ) value of n AS3600:2018 is larger than ACI318M up to 80MPa, but in the case of high strength grades over 80MPa, it is reversed and the ACI318M’s value is slightly larger than AS3600:2018’s.
For the moment factor, except for the low-strength grade below 10MPa, the moment factor of ACI318M is larger than AS3600:2018.
If you want to keep reading this article, please download the VOL.15 White Paper below.
 Banner Title Products
Banner Title Products