OVERVIEW
A structural engineer will have to analyze and design many unique and innovative structures. Some of these structures cannot be defined with specific stories or slabs using floor diaphragms; therefore, the application of static seismic loads or wind loads is not possible.
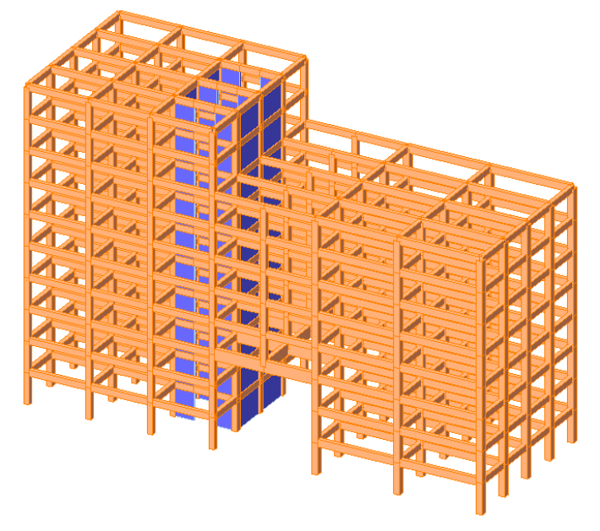
The following discussion will explain how to analyze and design structures where floor diaphragms cannot be defined, or where a story consists of two-floor diaphragms. Examples of these cases are illustrated in Figures 1a and 1b.
This material will discuss the following sections:
-
How to use the Nodal Body Force function to apply a static seismic load for a slab that cannot be defined as a floor diaphragm
-
How to use the Nodal Body Force function to apply a static seismic load for a steel structure with no slabs
-
How to use the Nodal Body Force function to apply a static seismic load for a structure where a story consists of two-floor diaphragms
-
Comparison of analysis results between two cases: The structure which uses floor diaphragms and the structure which does not use floor diaphragms
Structures Using the Nodal Body Functions
The Nodal Body Functions Used to Apply Static Seismic Load for a Slab
How to use the nodal body force function to apply static seismic load for a slab that cannot be defined as a floor diaphragm:
The Nodal Body Force function can be used to define masses as loads in any direction. Options which consider masses are the Nodal Mass, Load to Mass and Structure Mass options. When the Nodal Body Force function is used, an equivalent static seismic load can be defined using the mass of the structure.
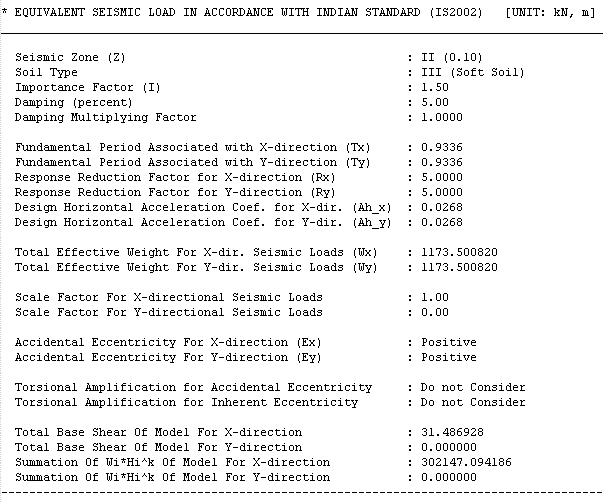
The static seismic load is calculated using the base shear force as per IS 1893:2002. Part 1 of this code, section 7.5.3 Design Seismic Shear Force states:
Vb=Ah×W
In the above equation, the base shear force (Vb) is calculated using the mass (W=mg) and the design horizontal seismic coefficient (Ah). The design horizontal seismic coefficient (Ah) is calculated using the zone factor (Z), the importance factor (I), the response reduction factor (R), and the average response acceleration coefficient (Sa/g).
Ah=(Z×I×Sa)/(2×R×g)
The following is a description for defining a static seismic load using the Nodal Body Force function:
Obtain the design horizontal seismic coefficient (Ah), and enter it as the Nodal Body Force Factor for the corresponding direction. Ah is known when selecting Loads > Lateral Loads > Static Seismic Loads. For a defined load case, select Seismic Load Profile, and then select Make Seismic Load Calc. Sheet (Refer to Figure 2). The mass is automatically calculated using the defined mass (Nodal Mass, Load to Mass, Structure Mass), and the static seismic load is calculated for each node.
midas Gen only requires the input of the design horizontal seismic coefficient to define a static seismic load using the Nodal Body Force function.
Figure 2. Seismic Load Calc. Sheet
The Nodal Body Functions Used to Apply Static Seismic Load for a Steel Structure
How to use the nodal body force function to apply static seismic load for a steel structure with no slabs:
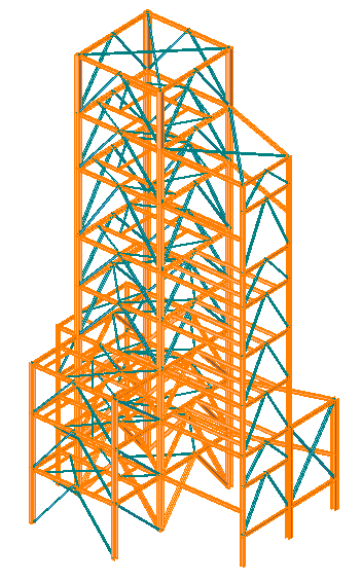
The 8-story steel structure has a steel-braced frame subjected to a lateral load. It is a structure consisting of brace members between each story, as shown in Figure 3. Because there are no slabs in the structure, the floors cannot be defined using floor diaphragms.

∙ Design Horizontal Seismic Coefficient (Ah) = 0.0268
∙ Response Reduction Factor = 5.0
∙ Zone Factor = 0.1
∙ Importance Factor (I) = 1.5
∙ Fundamental Period (T) = 0.075h (3/4) = 0.9336
Ah=(Z×I×Sa)/(2×R×g)
∙ Mass (m) = 122.1 kN/g
∙ Base Shear Force (Vb) = 1.12x106 N
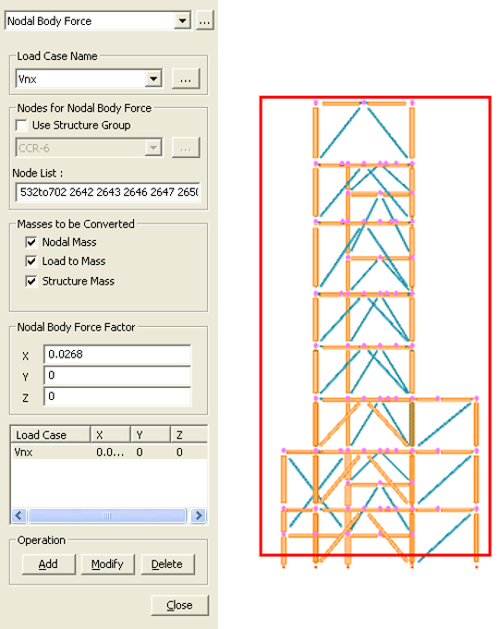

While defining the static seismic load using the Nodal Body Force function, as shown in Figure 4, use Select by Window to select the nodes of the structure to add to the Node List. Also, enter the calculated design horizontal seismic coefficient displayed in the Seismic Load Calc. Sheet as the Nodal Body Force Factor.
The base shear force is calculated by multiplying the weight (Wi) with the design horizontal seismic coefficient (Ah). The base shear force is distributed to each node as the static seismic load on the structure. When the static seismic load is applied at the nodes using the Nodal Body Force function, the static seismic load is divided into the mass at each node. The resulting application of the static seismic load on the steel structure is displayed in Figure 5.
Table 1 compares the reaction forces (EX, EY) due to the static seismic load when slabs are defined with floor diaphragms, to reaction forces (Vnx, Vny) due to the static seismic load when the Nodal Body Force function is used. Both procedures generate the same results.

This method is useful in applying a static seismic load for a steel structure with no definite floor diaphragms or a clear division of stories.
If you would like to keep reading this article, please download the VOL.12 White Paper below.
 Banner Title Products
Banner Title Products