Banner Title Products
MIDAS/Gen Analysis Options - Part 1.
You can download E-book for MIDAS/Gen Analysis Options - Part 1, After filling out the form at the end of this page.
Linear Static Analysis
The basic equation adopted in MIDAS/Gen for linear static analysis is as follows:
[K]{U}={P}
Where,
[K]: Stiffness Matrix
{U}: Displacement Vector
{P}: Load Vector
MIDAS/Gen allows unlimited numbers of static load cases and load combinations.
Figure 1. Flow Chart for Linear Static Analysis in MIDAS/Gen
Free Vibration Analysis
Eigenvalue Analysis
Mode shapes and natural periods of an undamped free vibration are obtained from the characteristic equation below.
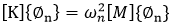
Where,
Eigenvalue analysis is also referred to as “free vibration analysis” and is used to analyze the dynamic characteristics of structures.
The dynamic characteristics obtained by an eigenvalue analysis include vibration modes (mode shapes), natural periods of vibration (natural frequencies), and modal participation factors. They are determined by the mass and stiffness of a structure.
Vibration modes take the form of natural shapes in which a structure freely vibrates or deforms. The first mode shape or natural vibration shape is identified by a shape that can be deformed with the least energy or force. The shapes formed with increases in energy define the subsequent higher modes.
Figure 2 shows the vibration modes of a cantilever beam arranged in the order of their energy requirements for deflected shapes, starting from the shape formed by the least energy.
A natural period of vibration is the time required to complete one full cycle of the free vibration motion in the corresponding natural mode.
The following describes the method of obtaining the natural period of a single degree of freedom (SDOF) system: Assuming zero damping and force in the governing motion equation of an SDOF system, we can obtain the 2nd order linear differential equation <Eq. 1> representing a free vibration.
<Eq. 1>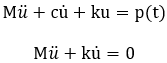
Since u is the displacement due to vibration, if we simply assume u = Acosωt, where, A is a constant related to the initial displacement, can be written as
<Eq. 2>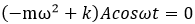
In order to satisfy the <Eq. 2>, the value of the parenthesis must be zero, which leads to <Eq. 3>.
<Eq. 3>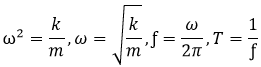
where, ω2, ω, f and T are eigenvalues, rotational natural frequency, natural frequency, and natural period respectively.
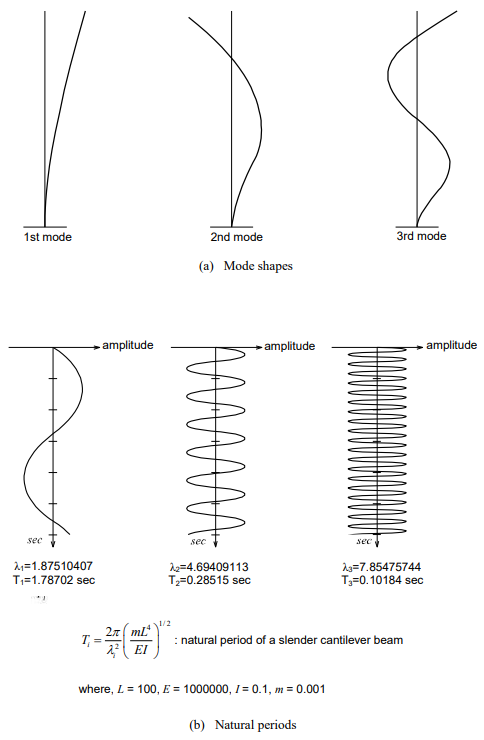
Figure 2. Mode Shapes and Corresponding Natural Periods of a Prismatic Cantilever Beam
The modal participation factor is expressed as a contribution ratio of the corresponding mode to the total modes and is written as
<Eq. 4>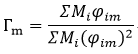
Where,
In most seismic design codes, it is stipulated that the sum of the effective modal masses included in an analysis should be greater than 90% of the total mass. This will ensure that the critical modes that affect the results are included in the design.
<Eq. 5>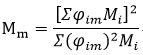
Where, Mm: Effective modal mass
If certain degrees of freedom of a given mass becomes constrained, the mass will be included in the total mass but excluded from the effective modal mass due to the restraints on the corresponding mode vectors. Accordingly, when you attempt to compare the effective modal mass with the total mass, the degrees of freedom pertaining to the mass components must not be constrained.
For instance, when the lateral displacement d.o.f. of a building basement is constrained, it is not necessary to enter the lateral mass components at the corresponding floors
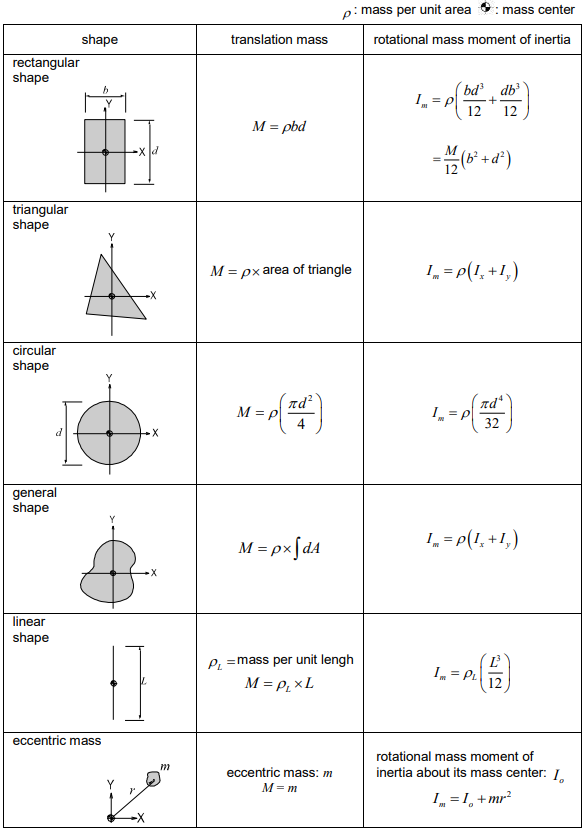
In order to analyze the dynamic behavior of a structure accurately, the analysis must closely reflect the mass and stiffness, which are the important factors to determine the eigenvalues. In most cases, finite element models can readily estimate the stiffness components of structural members. In the case of mass, however, you are required to pay particular attention to an accurate estimate.
The masses pertaining to the self-weights of structural components are relatively small compared to the total mass. It is quite important that an eigenvalue analysis accounts for all mass components in a structure, such as floor slabs and claddings among other masses.
Mass components are generally specified as 3 translational masses and 3 rotational mass moments of inertia consistent with 6 degrees of freedom per node. The rotational mass moments of inertia pertaining to rotational mass inertia do not directly affect the dynamic response of a structure.
Only translational ground accelerations are typically applied in a seismic design. However, when the structure is of an irregular shape, where the mass center does not coincide with the stiffness center, the rotational mass moments of inertia indirectly affect the dynamic response by changing the mode shapes.
Mass components are calculated by the following equations: (See Figure 3)
Translational mass : ∫dmWhere, r is the distance from the total mass center to the center of an infinitesimal mass.
The units for mass and rotational mass moment of inertia are defined by the unit of weights divided by the gravitational acceleration, W(T2/L), and the unit of masses multiplied by the square of a length unit, W(T2/L)×L2 respectively. Here, W, T, and L represent weight, time, and length units respectively. In the case of an MKS or English unit system, the mass is determined by the weight divided by the gravitational acceleration.
The masses in an SI unit system directly use the weights in the MKS units, whereas the stiffness or loads in the MKS units are multiplied by the gravitational acceleration for the SI unit system.
MIDAS/Gen uses lumped masses in analyses for efficiency. Mass data can be entered in the main menu through Model>Masses>Nodal Masses, Floor Diaphragm Masses or Loads to Masses.
MIDAS/Gen adopts the subspace iteration method for the solution of an eigenvalue analysis, which is suitable for the analyses of large structures.
Ritz Vector Analysis
Ritz vector analysis is an approach, which finds natural frequencies and mode shapes representing the dynamic properties of a structure. The use of Ritz vectors is known to be more efficient than using Eigenvector analysis for calculating such dynamic properties.
This method is an extension of the Rayleigh-Ritz approach, which finds a natural frequency by assuming a mode shape of a multi-degree of freedom structure and converting it into a single degree of freedom system.
We now assume that the displacement vector in the equation of motion for a structure of n – degrees of freedom can be expressed by combining p number of Ritz vectors. Here, p is smaller than or equal to n.
Where,
From the above assumption, the equation of motion of n – degrees of freedom can be reduced to the equation of motion of p – degrees of freedom.
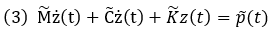Where,
The following eigenvalue is formulated and analyzed for the reduced equation of motion:
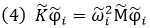Where,
Using the above eigenvalue solution and assuming the classical damping matrix, the reduced equation of motion can be decomposed into the equation of motion for a single degree of freedom for each mode as follows:
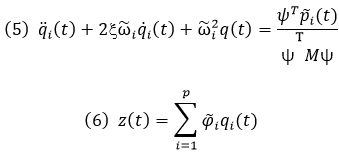Where,
The eigenvalue solution of the reduced equation of motion, φ ̃i, represents an approximate solution for the natural frequency of the original equation of motion.
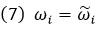Where,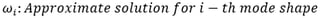
A mode shape of a structure is a vector, which defines the mapping relationship between the displacement vector of the equation of motion and the mode coordinate. The approximate mode shape obtained by Ritz vector analysis is thus defined by the relationship between the displacement vector of the original equation of motion, u(t), and the mode coordinate, qi(t), as noted below.
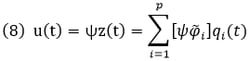
Accordingly, the approximate solution for the i – th mode shape is defined as
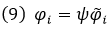Where,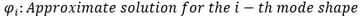
The approximate mode shape vector in Ritz vector analysis retains orthogonality for the original mass and stiffness matrices similar to that for eigenvalue analysis.
The approximate solution for natural frequencies and mode shapes in Ritz vector analysis is used for calculating modal participation factors and effective modal masses similar to a conventional eigenvalue analysis.
When a time history analysis is carried out by modal superposition on the basis of the results of Ritz vector analysis, the above equation of motion (5) is used.
The Ritz vector, which assumes the deformed shape of a structure, is generally created by repeatedly calculating the displacement due to loads applied to the structure. The user first specifies the initial load vector.
The basic assumption here is that the dynamic loading changes with time, but the spatial distribution for each degree of freedom follows the initial load vector specified by the user. Next, the first Ritz vector is obtained by performing the first static analysis for the specified initial load vector.
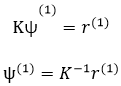Where,
The first Ritz vector thus obtained is assumed as the structural displacement However, the above static analysis ignores the effect of the inertia force developed by the dynamic response of the structure. Accordingly, the displacement due to the inertia force is calculated through additional repeated calculations.
The distribution of acceleration for the structure is assumed to follow the displacement vector calculated before, which is the first Ritz vector. The inertia force generated by the acceleration is calculated by multiplying the mass vector. The inertia force is then assumed to act as a loading, which induces additional displacement in the structure, and static analysis is carried out again.
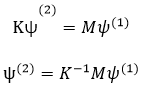
Where,
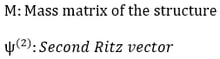
The second Ritz vector thus obtained in the above equation also reflects a static equilibrium only. Assuming the above equation is expressed without considering the acceleration distribution, the above process is repeated in order to calculate the number of Ritz vectors specified by the user.
The user may specify a multiple number of initial load vectors. The number of Ritz vectors to be generated can be individually specified for each initial load vector. However, the total number of Ritz vectors to be generated cannot exceed that of real modes, which exist in the equation of motion.
Also, those Ritz vectors already generated in the repetitive process are deleted once linearly dependent Ritz vectors are calculated. For this reason, the generation cycle ends if linearly independent Ritz vectors cannot be calculated any longer. This means that the initial load vectors specified by the user alone cannot find the specified number of modes.
The initial load vectors that can be specified in the MIDAS programs are an inertia force due to ground acceleration in the global X, Y or Z direction, a user-defined static load case and a nonlinear link force vector. The inertia force due to ground acceleration in the global X, Y or Z direction is mainly used to find the Ritz vector related to the displacement resulting from the ground acceleration in the corresponding direction.
The user-defined static load case is used to find the Ritz vectors for a dynamic load with specific distribution. A common static load case (dead load, live load, wind load, etc.) may be used, or an artificially created static load case may be used to generate Ritz vectors.
The member force vectors of nonlinear link elements are used to generate Ritz vectors. The member forces generated in each nonlinear link element are applied to the structure as a load vector. For only the degrees of freedom checked by the user among the 6 degrees of freedom in an element, initial load vectors having unit forces individually are composed and used for generating the Ritz vectors.
However, the member force vectors of link elements do not have to be used in the analysis of a structure, which contains nonlinear link elements. The user specifies initial load vectors at his/her discretion, which should adequately reflect the structural deformed shape under the given analysis condition.
When compared with eigenvalue analysis, Ritz vector analysis has the following advantages:
Ritz vectors are founded on static analysis solutions for real loads. Even if smaller numbers of modes are calculated in Ritz vector analysis, the effects of higher modes are automatically reflected. For example, the first mode shape in a Ritz vector analysis can be different from that in an eigenvalue analysis, which is attributed to representing the effects of higher modes.
Also, Ritz vector analysis finds only the mode shapes pertaining to the loads acting on the structure, thereby eliminating the calculations for unnecessary modes. Ritz vector analysis thus reduces the number of modes for finding accurate results. Ritz vector analysis requires a less number of modes to attain sufficient modal mass participation compared to eigenvalue analysis.
Considerations of Damping
Structural damping in a dynamic analysis can be largely classified into the following:
▶Modal damping
∙ Proportional Damping
- Mass Proportional Type
- Stiffness proportional Type
- Rayleigh Type
- Caughey Type
∙ Non-Proportional Damping
- Energy Proportional Type
▶Viscous Damping (Voigt Model & Maxwell Model)
▶Hysteretic Damping
▶Friction Damping
∙ Internal Friction Damping (Material Damping)
∙ External Friction Damping
∙ Sliding Friction Damping
▶Radiation Damping
Among the many different ways of expressing damping phenomena above, modal damping is most frequently used in numerical analyses of structures. The values for modal damping are determined for each modal natural frequency of a vibration system. The modal damping can be classified into proportional and non-proportional damping.
The MIDAS programs provide proportional damping, which includes mass proportional, stiffness proportional and Rayleigh type damping
* If you would like to see more information for the Damping, please fill out the form below and download WHITE PAPER for MIDAS/Gen Analysis Options - Part 1.😉
